谨以此文献给大连海事大学的吴楠老师,柳晓鸣老师,王新年老师以及张晶泊老师。
完整版请查看我的知乎专栏:
四、傅里叶变换(Fourier Tranformation)
相信通过前面三章,大家对频域以及傅里叶级数都有了一个全新的认识。但是文章在一开始关于钢琴琴谱的例子我曾说过,这个栗子是一个公式错误,但是概念典型的例子。所谓的公式错误在哪里呢?
傅里叶级数的本质是将一个周期的信号分解成无限多分开的(离散的)正弦波,但是宇宙似乎并不是周期的。曾经在学数字信号处理的时候写过一首打油诗:
往昔连续非周期,
回忆周期不连续,
任你ZT、DFT,
还原不回去。
(请无视我渣一样的文学水平……)
在这个世界上,有的事情一期一会,永不再来,并且时间始终不曾停息地将那些刻骨铭心的往昔连续的标记在时间点上。但是这些事情往往又成为了我们格外宝贵的回忆,在我们大脑里隔一段时间就会周期性的蹦出来一下,可惜这些回忆都是零散的片段,往往只有最幸福的回忆,而平淡的回忆则逐渐被我们忘却。因为,往昔是一个连续的非周期信号,而回忆是一个周期离散信号。
是否有一种数学工具将连续非周期信号变换为周期离散信号呢?抱歉,真没有。
比如傅里叶级数,在时域是一个周期且连续的函数,而在频域是一个非周期离散的函数。这句话比较绕嘴,实在看着费事可以干脆回忆第一章的图片。
而在我们接下去要讲的傅里叶变换,则是将一个时域非周期的连续信号,转换为一个非周期连续信号。
算了,还是上一张图方便大家理解吧:
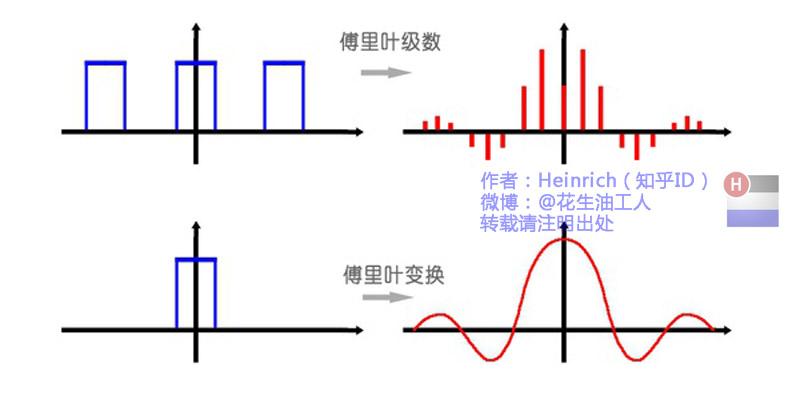
所以说,钢琴谱其实并非一个连续的频谱,而是很多在时间上离散的频率,但是这样的一个贴切的比喻真的是很难找出第二个来了。
因此在傅里叶变换在频域上就从离散谱变成了连续谱。那么连续谱是什么样子呢?
你见过大海么?
为了方便大家对比,我们这次从另一个角度来看频谱,还是傅里叶级数中用到最多的那幅图,我们从频率较高的方向看。
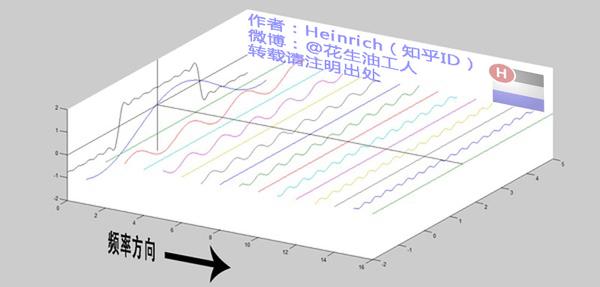
尽情的发挥你的想象,想象这些离散的正弦波离得越来越近,逐渐变得连续……
直到变得像波涛起伏的大海:
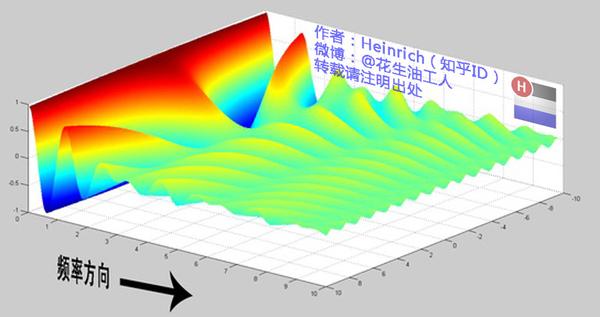
很抱歉,为了能让这些波浪更清晰的看到,我没有选用正确的计算参数,而是选择了一些让图片更美观的参数,不然这图看起来就像屎一样了。
不过通过这样两幅图去比较,大家应该可以理解如何从离散谱变成了连续谱的了吧?原来离散谱的叠加,变成了连续谱的累积。所以在计算上也从求和符号变成了积分符号。
不过,这个故事还没有讲完,接下去,我保证让你看到一幅比上图更美丽壮观的图片,但是这里需要介绍到一个数学工具才能然故事继续,这个工具就是——
五、宇宙耍帅第一公式:欧拉公式
虚数i这个概念大家在高中就接触过,但那时我们只知道它是-1的平方根,可是它真正的意义是什么呢?
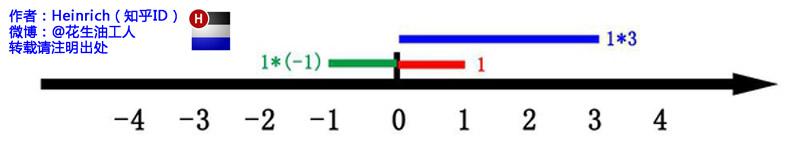 这里有一条数轴,在数轴上有一个红色的线段,它的长度是1。当它乘以3的时候,它的长度发生了变化,变成了蓝色的线段,而当它乘以-1的时候,就变成了绿色的线段,或者说线段在数轴上围绕原点旋转了180度。
这里有一条数轴,在数轴上有一个红色的线段,它的长度是1。当它乘以3的时候,它的长度发生了变化,变成了蓝色的线段,而当它乘以-1的时候,就变成了绿色的线段,或者说线段在数轴上围绕原点旋转了180度。
我们知道乘-1其实就是乘了两次 i使线段旋转了180度,那么乘一次 i 呢——答案很简单——旋转了90度。
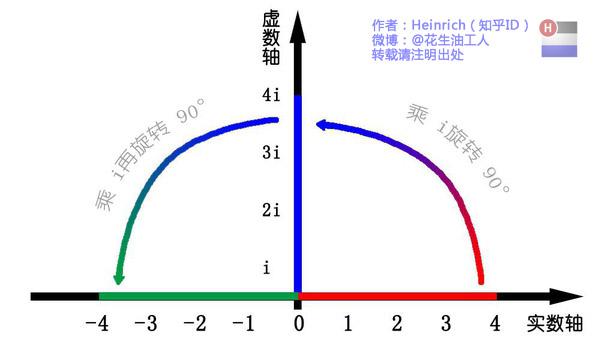
现在,就有请宇宙第一耍帅公式欧拉公式隆重登场——
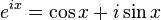 这个公式在数学领域的意义要远大于傅里叶分析,但是乘它为宇宙第一耍帅公式是因为它的特殊形式——当x等于Pi的时候。
这个公式在数学领域的意义要远大于傅里叶分析,但是乘它为宇宙第一耍帅公式是因为它的特殊形式——当x等于Pi的时候。
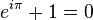 经常有理工科的学生为了跟妹子表现自己的学术功底,用这个公式来给妹子解释数学之美:”石榴姐你看,这个公式里既有自然底数e,自然数1和0,虚数i还有圆周率pi,它是这么简洁,这么美丽啊!“但是姑娘们心里往往只有一句话:”臭屌丝……“
经常有理工科的学生为了跟妹子表现自己的学术功底,用这个公式来给妹子解释数学之美:”石榴姐你看,这个公式里既有自然底数e,自然数1和0,虚数i还有圆周率pi,它是这么简洁,这么美丽啊!“但是姑娘们心里往往只有一句话:”臭屌丝……“
这个公式关键的作用,是将正弦波统一成了简单的指数形式。我们来看看图像上的涵义:
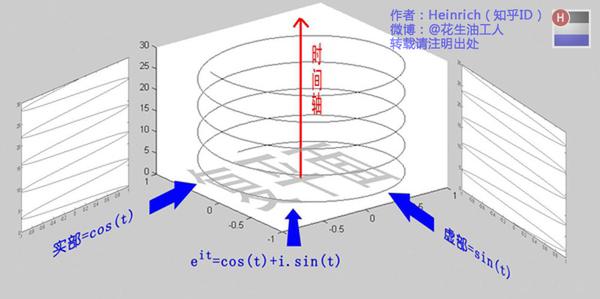
关于复数更深的理解,大家可以参考:
这里不需要讲的太复杂,足够让大家理解后面的内容就可以了。
六、指数形式的傅里叶变换
有了欧拉公式的帮助,我们便知道:正弦波的叠加,也可以理解为螺旋线的叠加在实数空间的投影。而螺旋线的叠加如果用一个形象的栗子来理解是什么呢?
光波
高中时我们就学过,自然光是由不同颜色的光叠加而成的,而最著名的实验就是牛顿师傅的三棱镜实验:
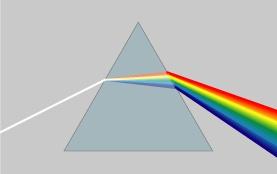
但不同的是,傅里叶变换出来的频谱不仅仅是可见光这样频率范围有限的叠加,而是频率从0到无穷所有频率的组合。
这里,我们可以用两种方法来理解正弦波:
第一种前面已经讲过了,就是螺旋线在实轴的投影。
另一种需要借助欧拉公式的另一种形式去理解:
将以上两式相加再除2,得到:
这个式子可以怎么理解呢?
我们刚才讲过,e^(it)可以理解为一条逆时针旋转的螺旋线,那么e^(-it)则可以理解为一条顺时针旋转的螺旋线。而cos(t)则是这两条旋转方向不同的螺旋线叠加的一半,因为这两条螺旋线的虚数部分相互抵消掉了!
举个例子的话,就是极化方向不同的两束光波,磁场抵消,电场加倍。
这里,逆时针旋转的我们称为正频率,而顺时针旋转的我们称为负频率(注意不是复频率)。
好了,刚才我们已经看到了大海——连续的傅里叶变换频谱,现在想一想,连续的螺旋线会是什么样子:
想象一下再往下翻:
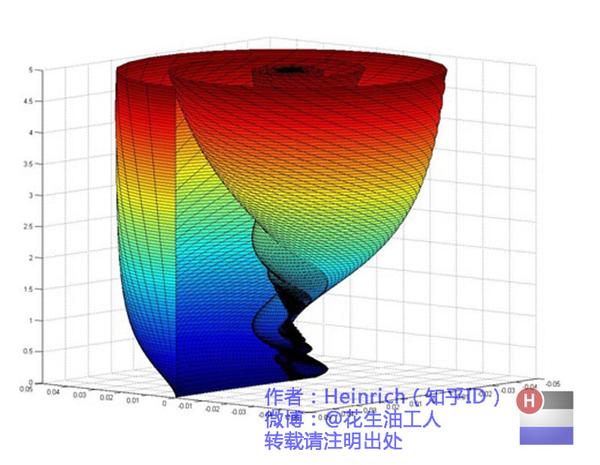
你猜猜,这个图形在时域是什么样子?
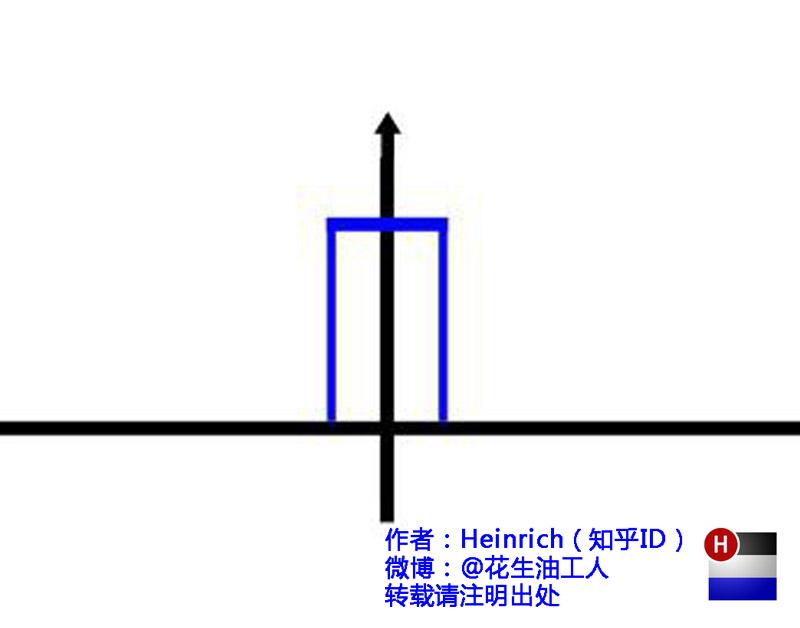
顺便说一句,那个像大海螺一样的图,为了方便观看,我仅仅展示了其中正频率的部分,负频率的部分没有显示出来。
如果你认真去看,海螺图上的每一条螺旋线都是可以清楚的看到的,每一条螺旋线都有着不同的振幅(旋转半径),频率(旋转周期)以及相位。而将所有螺旋线连成平面,就是这幅海螺图了。
好了,讲到这里,相信大家对傅里叶变换以及傅里叶级数都有了一个形象的理解了,我们最后用一张图来总结一下:
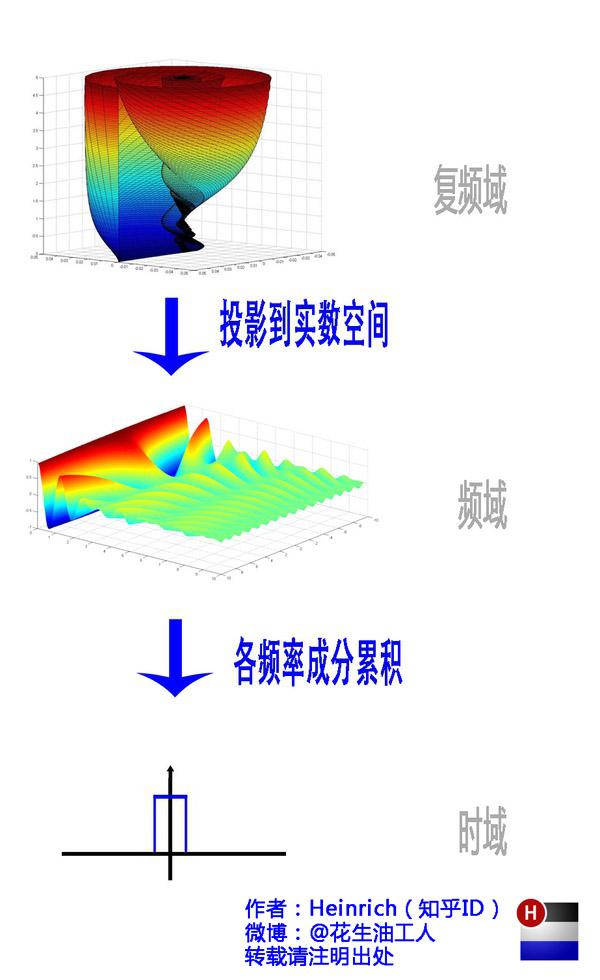
好了,傅里叶的故事终于讲完了,下面来讲讲我的故事:
这篇文章第一次被卸下来的地方你们绝对猜不到在哪,是在一张高数考试的卷子上。当时为了刷分,我重修了高数(上),但是后来时间紧压根没复习,所以我就抱着裸考的心态去了考场。但是到了考场我突然意识到,无论如何我都不会比上次考的更好了,所以干脆写一些自己对于数学的想法吧。于是用了一个小时左右的时间在试卷上洋洋洒洒写了本文的第一草稿。
你们猜我的了多少分?
6分
没错,就是这个数字。而这6分的成绩是因为最后我实在无聊,把选择题全部填上了C,应该是中了两道,得到了这宝贵的6分。说真的,我很希望那张卷子还在,但是应该不太可能了。
那么你们猜猜我第一次信号与系统考了多少分呢?
45分
没错,刚刚够参加补考的。但是我心一横没去考,决定重修。因为那个学期在忙其他事情,学习真的就抛在脑后了。但是我知道这是一门很重要的课,无论如何我要吃透它。说真的,信号与系统这门课几乎是大部分工科课程的基础,尤其是通信专业。
在重修的过程中,我仔细分析了每一个公式,试图给这个公式以一个直观的理解。虽然我知道对于研究数学的人来说,这样的学习方法完全没有前途可言,因为随着概念愈加抽象,维度越来越高,这种图像或者模型理解法将完全丧失作用。但是对于一个工科生来说,足够了。
后来来了德国,这边学校要求我重修信号与系统时,我彻底无语了。但是没办法,德国人有时对中国人就是有种藐视,觉得你的教育不靠谱。所以没办法,再来一遍吧。
这次,我考了满分,而及格率只有一半。
老实说,数学工具对于工科生和对于理科生来说,意义是完全不同的。工科生只要理解了,会用,会查,就足够了。但是很多高校却将这些重要的数学课程教给数学系的老师去教。这样就出现一个问题,数学老师讲得天花乱坠,又是推理又是证明,但是学生心里就只有一句话:学这货到底干嘛用的?
缺少了目标的教育是彻底的失败。
在开始学习一门数学工具的时候,学生完全不知道这个工具的作用,现实涵义。而教材上有只有晦涩难懂,定语就二十几个字的概念以及看了就眼晕的公式。能学出兴趣来就怪了!
好在我很幸运,遇到了大连海事大学的吴楠老师。他的课全程来看是两条线索,一条从上而下,一条从下而上。先将本门课程的意义,然后指出这门课程中会遇到哪样的问题,让学生知道自己学习的某种知识在现实中扮演的角色。然后再从基础讲起,梳理知识树,直到延伸到另一条线索中提出的问题,完美的衔接在一起!
这样的教学模式,我想才是大学里应该出现的。
最后,写给所有给我点赞并留言的同学。真的谢谢大家的支持,也很抱歉不能一一回复。因为知乎专栏的留言要逐次加载,为了看到最后一条要点很多次加载。当然我都坚持看完了,只是没办法一一回复。
本文只是介绍了一种对傅里叶分析新颖的理解方法,对于求学,还是要踏踏实实弄清楚公式和概念,学习,真的没有捷径。但至少通过本文,我希望可以让这条漫长的路变得有意思一些。
最后,祝大家都能在学习中找到乐趣。
———————————————
转载请保留版权信息
作 者:韩 昊
知 乎:Heinrich
微 博:@花生油工人
知乎专栏:与时间无关的故事
from:http://daily.zhihu.com/story/3955477